Momentum

From Wikipedia, the free encyclopedia

Jump to: navigation, search

This article is about momentum in physics. For other uses, see Momentum (disambiguation).


In a game of pool, momentum is conserved; that is, if one ball stops dead after the collision, the other ball will continue away with all the momentum. If the moving ball continues or is deflected then both balls will carry a portion of the momentum from the collision,
Common symbol(s):	p, p
SI unit:	kg m/s or N s

Classical mechanics
History Timeline
Branches[show]
Formulations[show]
Fundamental concepts[show]
Core topics[show]
Rotational motion [show]
Scientists[show]
v t e

In classical mechanics, linear momentum or translational momentum (pl. momenta; SI unit kg m/s, or equivalently, N s) is the product of the mass and velocity of an object. For example, a heavy truck moving fast has a large momentum—it takes a large and prolonged force to get the truck up to this speed, and it takes a large and prolonged force to bring it to a stop afterwards. If the truck were lighter, or moving more slowly, then it would have less momentum.
Like velocity, linear momentum is a vector quantity, possessing a direction as well as a magnitude:

$\mathbf{p} = m \mathbf{v}.$

Linear momentum is also a conserved quantity, meaning that if a closed system is not affected by external forces, its total linear momentum cannot change. In classical mechanics, conservation of linear momentum is implied by Newton's laws; but it also holds in special relativity (with a modified formula) and, with appropriate definitions, a (generalized) linear momentum conservation law holds in electrodynamics, quantum mechanics, quantum field theory, and general relativity.

Newtonian mechanics

Momentum has a direction as well as magnitude. Quantities that have both a magnitude and a direction are known as vector quantities. Because momentum has a direction, it can be used to predict the resulting direction of objects after they collide, as well as their speeds. Below, the basic properties of momentum are described in one dimension. The vector equations are almost identical to the scalar equations (see multiple dimensions).

Single particle

The momentum of a particle is traditionally represented by the letter

p

. It is the product of two quantities, the mass (represented by the letter

m

) and velocity (

v

):^[1]

$p = m v.$

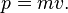
The units of momentum are the product of the units of mass and velocity. In SI units, if the mass is in kilograms and the velocity in meters per second, then the momentum is in kilograms meters/second (kg m/s). Being a vector, momentum has magnitude and direction. For example, a model airplane of 1 kg, traveling due north at 1 m/s in straight and level flight, has a momentum of 1 kg m/s due north measured from the ground.

Many particles

The momentum of a system of particles is the sum of their momenta. If two particles have masses

m 1

and

m 2

, and velocities

v 1

and

v 2

, the total momentum is

$\begin{align} p &= p_1 + p_2 \\ &= m_1 v_1 + m_2 v_2\,. \end{align}$

The momenta of more than two particles can be added in the same way.
A system of particles has a center of mass, a point determined by the weighted sum of their positions:

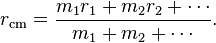
$r_\text{cm} = \frac{m_1 r_1 + m_2 r_2 + \cdots}{m_1 + m_2 + \cdots}.$

If all the particles are moving, the center of mass will generally be moving as well. If the center of mass is moving at velocity

v cm

, the momentum is:

$p= mv_\text{cm}.$

This is known as Euler's first law.^[2]^[3]

Relation to force

If a force

F

is applied to a particle for a time interval

Δ t

, the momentum of the particle changes by an amount

$\Delta p = F \Delta t\,.$

In differential form, this gives Newton's second law: the rate of change of the momentum of a particle is equal to the force

F

acting on it:^[1]

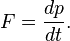
$F = \frac{dp }{d t}.$

If the force depends on time, the change in momentum (or impulse) between times

t 1

and

t 2

$\Delta p = \int_{t_1}^{t_2} F(t)\, dt\,.$

The second law only applies to a particle that does not exchange matter with its surroundings,^[4] and so it is equivalent to write

$F = m\frac{dv}{d t} = m a,$

so the force is equal to mass times acceleration.^[1]
Example: a model airplane of 1 kg accelerates from rest to a velocity of 6 m/s due north in 2 s. The thrust required to produce this acceleration is 3 newton. The change in momentum is 6 kg m/s. The rate of change of momentum is 3 (kg m/s)/s = 3 N.

Conservation

A Newton's cradle demonstrates conservation of momentum.

In a closed system (one that does not exchange any matter with the outside and is not acted on by outside forces) the total momentum is constant. This fact, known as the law of conservation of momentum, is implied by Newton's laws of motion.^[5] Suppose, for example, that two particles interact. Because of the third law, the forces between them are equal and opposite. If the particles are numbered 1 and 2, the second law states that

F 1 = dp 1 / dt

and

F 2 = dp 2 / dt

. Therefore

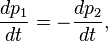
$\frac{d p_1}{d t} = - \frac{d p_2}{d t},$

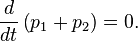
$\frac{d}{d t} \left(p_1+ p_2\right)= 0.$

If the velocities of the particles are

u 1

and

u 2

before the interaction, and afterwards they are

v 1

and

v 2

, then

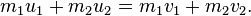
$m_1 u_{1} + m_2 u_{2} = m_1 v_{1} + m_2 v_{2}.$

This law holds no matter how complicated the force is between particles. Similarly, if there are several particles, the momentum exchanged between each pair of particles adds up to zero, so the total change in momentum is zero. This conservation law applies to all interactions, including collisions and separations caused by explosive forces.^[5] It can also be generalized to situations where Newton's laws do not hold, for example in the theory of relativity and in electrodynamics.^[6]

Dependence on reference frame

Newton's apple in Einstein's elevator. In person A's frame of reference, the apple has non-zero velocity and momentum. In the elevator's and person B's frames of reference, it has zero velocity and momentum.

Momentum is a measurable quantity, and the measurement depends on the motion of the observer. For example, if an apple is sitting in a glass elevator that is descending, an outside observer looking into the elevator sees the apple moving, so to that observer the apple has a nonzero momentum. To someone inside the elevator, the apple does not move, so it has zero momentum. The two observers each have a frame of reference in which they observe motions, and if the elevator is descending steadily they will see behavior that is consistent with the same physical laws.
Suppose a particle has position

x

in a stationary frame of reference. From the point of view of another frame of reference moving at a uniform speed

u

, the position (represented by a primed coordinate) changes with time as

$x' = x - ut\,.$

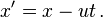
This is called a Galilean transformation. If the particle is moving at speed

dx/dt = v

in the first frame of reference, in the second it is moving at speed

$v' = \frac{dx'}{dt} = v-u\,.$

Since

u

does not change, the accelerations are the same:

$a' = \frac{dv'}{dt} = a\,.$

Thus, momentum is conserved in both reference frames. Moreover, as long as the force has the same form in both frames, Newton's second law is unchanged. Forces such as Newtonian gravity, which depend only on the scalar distance between objects, satisfy this criterion. This independence of reference frame is called Newtonian relativity or Galilean invariance.^[7]
A change of reference frame can often simplify calculations of motion. For example, in a collision of two particles a reference frame can be chosen where one particle begins at rest. Another commonly used reference frame is the center of mass frame, one that is moving with the center of mass. In this frame, the total momentum is zero.

Application to collisions

By itself, the law of conservation of momentum is not enough to determine the motion of particles after a collision. Another property of the motion, kinetic energy, must be known. This is not necessarily conserved. If it is conserved, the collision is called an elastic collision; if not, it is an inelastic collision.

Elastic collisions

Main article: Elastic collision

Elastic collision of equal masses

Elastic collision of unequal masses

An elastic collision is one in which no kinetic energy is lost. Perfectly elastic "collisions" can occur when the objects do not touch each other, as for example in atomic or nuclear scattering where electric repulsion keeps them apart. A slingshot maneuver of a satellite around a planet can also be viewed as a perfectly elastic collision from a distance. A collision between two pool balls is a good example of an almost totally elastic collision, due to their high rigidity; but when bodies come in contact there is always some dissipation.^[8]
A head-on elastic collision between two bodies can be represented by velocities in one dimension, along a line passing through the bodies. If the velocities are

u 1

and

u 2

before the collision and

v 1

and

v 2

after, the equations expressing conservation of momentum and kinetic energy are:

$\begin{align} m_1 u_1 + m_2 u_2 &= m_1 v_1 + m_2 v_2\\ \tfrac{1}{2} m_1 u_1^2 + \tfrac{1}{2} m_2 u_2^2 &= \tfrac{1}{2} m_1 v_1^2 + \tfrac{1}{2} m_2 v_2^2\,.\end{align}$

A change of reference frame can often simplify the analysis of a collision. For example, suppose there are two bodies of equal mass

m

, one stationary and one approaching the other at a speed

v

(as in the figure). The center of mass is moving at speed

v /2

and both bodies are moving towards it at speed

v /2

. Because of the symmetry, after the collision both must be moving away from the center of mass at the same speed. Adding the speed of the center of mass to both, we find that the body that was moving is now stopped and the other is moving away at speed

v

. The bodies have exchanged their velocities. Regardless of the velocities of the bodies, a switch to the center of mass frame leads us to the same conclusion. Therefore, the final velocities are given by^[5]

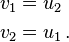
$\begin{align} v_1 &= u_2\\ v_2 &= u_1\,. \end{align}$

In general, when the initial velocities are known, the final velocities are given by^[9]

$v_{1} = \left( \frac{m_1 - m_2}{m_1 + m_2} \right) u_{1} + \left( \frac{2 m_2}{m_1 + m_2} \right) u_{2}\,$

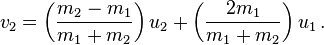
$v_{2} = \left( \frac{m_2 - m_1}{m_1 + m_2} \right) u_{2} + \left( \frac{2 m_1}{m_1 + m_2} \right) u_{1}\,.$

If one body has much greater mass than the other, its velocity will be little affected by a collision while the other body will experience a large change.

Inelastic collisions

Main article: Inelastic collision

a perfectly inelastic collision between equal masses

In an inelastic collision, some of the kinetic energy of the colliding bodies is converted into other forms of energy such as heat or sound. Examples include traffic collisions,^[10] in which the effect of lost kinetic energy can be seen in the damage to the vehicles; electrons losing some of their energy to atoms (as in the Franck–Hertz experiment);^[11] and particle accelerators in which the kinetic energy is converted into mass in the form of new particles.
In a perfectly inelastic collision (such as a bug hitting a windshield), both bodies have the same motion afterwards. If one body is motionless to begin with, the equation for conservation of momentum is

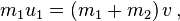
$m_1 u_1 = \left( m_1 + m_2 \right) v\,,$

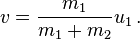
$v = \frac{m_1}{m_1+m_2} u_1\,.$

In a frame of reference moving at the speed

v)

, the objects are brought to rest by the collision and 100% of the kinetic energy is converted.
One measure of the inelasticity of the collision is the coefficient of restitution

C R

, defined as the ratio of relative velocity of separation to relative velocity of approach. In applying this measure to ball sports, this can be easily measured using the following formula:^[12]

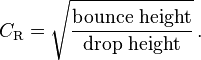
$C_\text{R} = \sqrt{\frac{\text{bounce height}}{\text{drop height}}}\,.$

The momentum and energy equations also apply to the motions of objects that begin together and then move apart. For example, an explosion is the result of a chain reaction that transforms potential energy stored in chemical, mechanical, or nuclear form into kinetic energy, acoustic energy, and electromagnetic radiation. Rockets also make use of conservation of momentum: propellant is thrust outward, gaining momentum, and an equal and opposite momentum is imparted to the rocket.^[13]

Multiple dimensions

Two-dimensional elastic collision. There is no motion perpendicular to the image, so only two components are needed to represent the velocities and momenta. The two blue vectors represent velocities after the collision and add vectorially to get the initial (red) velocity.

Real motion has both direction and magnitude and must be represented by a vector. In a coordinate system with

x, y, z

axes, velocity has components

v x

in the

x

direction,

v y

in the

y

direction,

v z

in the

z

direction. The vector is represented by a boldface symbol:^[14]

$\mathbf{v} = \left(v_x,v_y,v_z \right).$

Similarly, the momentum is a vector quantity and is represented by a boldface symbol:

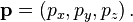
$\mathbf{p} = \left(p_x,p_y,p_z \right).$

The equations in the previous sections work in vector form if the scalars

p

and

v

are replaced by vectors

p

and

v

. Each vector equation represents three scalar equations. For example,

$\mathbf{p}= m \mathbf{v}$

represents three equations:^[14]

$\begin{align} p_x &= m v_x\\ p_y &= m v_y \\ p_z &= m v_z. \end{align}$

The kinetic energy equations are exceptions to the above replacement rule. The equations are still one-dimensional, but each scalar represents the magnitude of the vector, for example,

$v^2 = v_x^2+v_y^2+v_z^2\,.$

Each vector equation represents three scalar equations. Often coordinates can be chosen so that only two components are needed, as in the figure. Each component can be obtained separately and the results combined to produce a vector result.^[14]
A simple construction involving the center of mass frame can be used to show that if a stationary elastic sphere is struck by a moving sphere, the two will head off at right angles after the collision (as in the figure).^[15]

Objects of variable mass

The concept of momentum plays a fundamental role in explaining the behavior of variable-mass objects such as a rocket ejecting fuel or a star accreting gas. In analyzing such an object, one treats the object's mass as a function that varies with time:

m (t)

. The momentum of the object at time

t

is therefore

p (t) = m (t) v (t)

. One might then try to invoke Newton's second law of motion by saying that the external force

F

on the object is related to its momentum

p (t)

F = dp / dt

, but this is incorrect, as is the related expression found by applying the product rule to

d (mv)/ dt

:^[16]

$F = m(t) \frac{dv}{dt} + v(t) \frac{dm}{dt}. \qquad \mathrm{(wrong)}$

This equation does not correctly describe the motion of variable-mass objects. The correct equation is

$F = m(t) \frac{dv}{dt} - u \frac{dm}{dt},$

where

u

is the velocity of the ejected/accreted mass as seen in the object's rest frame.^[16] This is distinct from

v

, which is the velocity of the object itself as seen in an inertial frame.
This equation is derived by keeping track of both the momentum of the object as well as the momentum of the ejected/accreted mass. When considered together, the object and the mass constitute a closed system in which total momentum is conserved.

Generalized coordinates

Lagrangian mechanics

In Lagrangian mechanics, a Lagrangian is defined as the difference between the kinetic energy

T

and the potential energy

V

$\mathcal{L} = T-V\,.$

If the generalized coordinates are represented as a vector

q = (q 1, q 2, ... , q N)

and time differentiation is represented by a dot over the variable, then the equations of motion (known as the Lagrange or Euler–Lagrange equations) are a set of

N

equations:^[20]

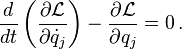
$\frac{d}{d t}\left(\frac{\partial \mathcal{L} }{\partial\dot{q}_j}\right) - \frac{\partial \mathcal{L}}{\partial q_j} = 0\,.$

If a coordinate

q i

is not a Cartesian coordinate, the associated generalized momentum component

p i

does not necessarily have the dimensions of linear momentum. Even if

q i

is a Cartesian coordinate,

p i

will not be the same as the mechanical momentum if the potential depends on velocity.^[6] Some sources represent the kinematic momentum by the symbol

Π

.^[21]
In this mathematical framework, a generalized momentum is associated with the generalized coordinates. Its components are defined as

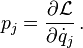
$p_j = \frac{\partial \mathcal{L} }{\partial \dot{q}_j}\,.$

Each component

p j

is said to be the conjugate momentum for the coordinate

q j

.
Now if a given coordinate

q i

does not appear in the Lagrangian (although its time derivative might appear), then

$p_j = \text{constant}\,.$

This is the generalization of the conservation of momentum.^[6]
Even if the generalized coordinates are just the ordinary spatial coordinates, the conjugate momenta are not necessarily the ordinary momentum coordinates. An example is found in the section on electromagnetism.

Hamiltonian mechanics

In Hamiltonian mechanics, the Lagrangian (a function of generalized coordinates and their derivatives) is replaced by a Hamiltonian that is a function of generalized coordinates and momentum. The Hamiltonian is defined as

$\mathcal{H}\left(\mathbf{q},\mathbf{p},t\right) = \mathbf{p}\cdot\dot{\mathbf{q}} - \mathcal{L}\left(\mathbf{q},\dot{\mathbf{q}},t\right)\,,$

Team One

Rabu, 04 Desember 2013

Momentum

Momentum

Contents

Newtonian mechanics

Single particle

Many particles

Relation to force

Conservation

Dependence on reference frame

Application to collisions

Elastic collisions

Inelastic collisions

Multiple dimensions

Objects of variable mass

Generalized coordinates

Lagrangian mechanics

Hamiltonian mechanics

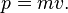
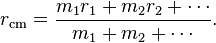
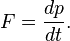
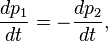
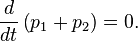
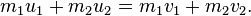
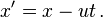
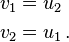
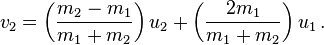
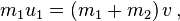
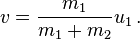
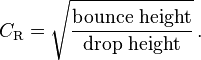
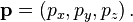
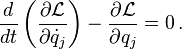
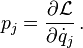
Tidak ada komentar:

Posting Komentar